第9章 数据统计分析案例
本章以案例为主,通过简单的知识讲解使读者了解数据统计分析中常用的分析方法,如对比分析,同比、定比和环比分析,贡献度分析,差异化分析,相关性分析和时间序列分析的概念。通过典型案例,将数据统计分析方法与前面学习的内容相结合,力求将所学内容应用到实践中。
9.1 对比分析
9.1.1 什么是对比分析
对比分析法是将两个或两个以上的数据进行比较,分析其中的差异,从而揭示这些事物代表的发展变化情况和规律性。
特点:非常直观地看出事物某方面的变化或差距,而且可以准确、量化地表示出变化的差距是多少。
对比分析法通常是把两个相互联系的指标数据进行比较,从数量上展示和说明研究对象规模的大小、水平的高低、速度的快慢,以及各种关系是否协调。对比分析一般来说有以下几种对比方法:纵向对比、横向对比、标准对比、实际与计划对比。
9.1.2 案例:对比分析各品牌销量表现TOP10
案例位置:资源包\MR\Code\09\example\01
对比国产各品牌汽车2020年1月销量,效果如图9.1所示。
程序代码如下:

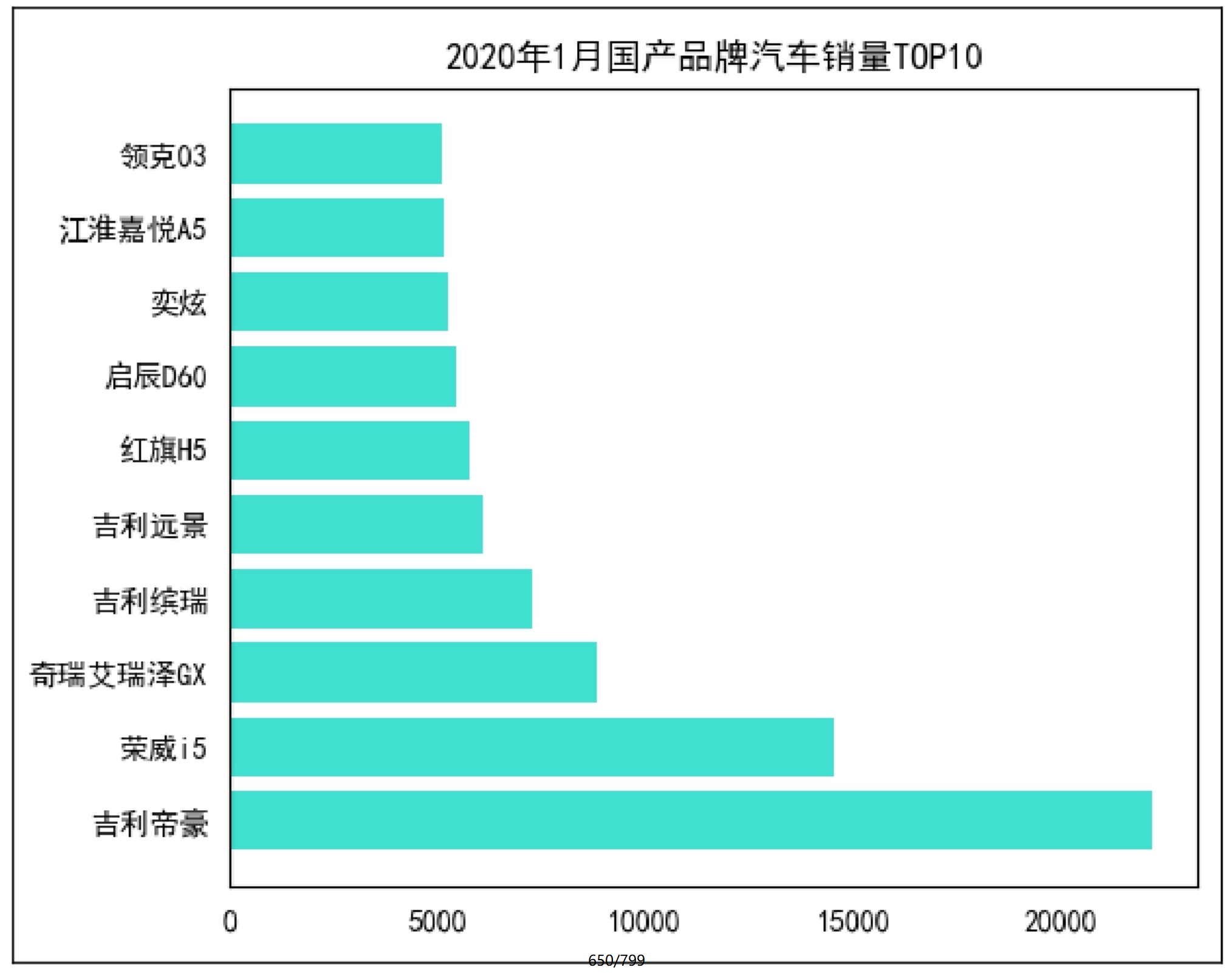
图9.1 对比分析各品牌销量表现TOP10
9.2 同比、定比和环比分析
在数据分析中,有一个重要的分析方法,叫趋势分析法,即将两期或连续数期报告中某一指标进行对比,确定其增减变动的方向、数额和幅度,以确定该指标的变动趋势。趋势分析法中的指标,有同比分析、定比(定基比)分析和环比分析,以及同比增长率分析、定比(定基比)增长率分析和环比增长率分析。
9.2.1 同比、定比和环比概述
首先了解一下同比、定比和环比的概念。
同比:本期数据与历史同期数据比较。例如,2021年11月份与2020年11月份相比较。
定比:本期数据与特定时期的数据比较。例如,2021年11月与2019年12月份相比较。
环比:本期数据与上期数据比较。例如,2021年11月份与2020年11月份相比较。
同比的好处是可以排除一部分季节因素;环比的好处是可以更直观地表明阶段性的变换,但是会受季节性因素影响;定比常用于财务数据分析。下面来看一个生活中经常出现的场景。 同比:去年这个这时候这条裙子我还能穿,现在穿不进去啦! 定比:年龄,50岁是25岁的两倍。 环比:这个月好像比上个月胖了。
下面简单介绍一下同比、定比和环比计算的公式。
1.同比
同比的计算公式如下:

2.定比
定比的计算公式如下:

3.环比
环比增长率反映本期比上期增长了多少,公式如下:

环比发展速度是本期水平与前一期水平之比,反映前后两期的发展变化情况,公式如下:

9.2.2 案例1:京东电商单品销量同比增长情况分析
案例位置:资源包\MR\Code\09\example\02\01
下面分析2020年2月与2019年2月相比,京东电商《零基础学Python(全彩版)》一书销量同比增长情况,效果如图9.2所示。
从分析结果得知:上海、武汉同比增长较小。
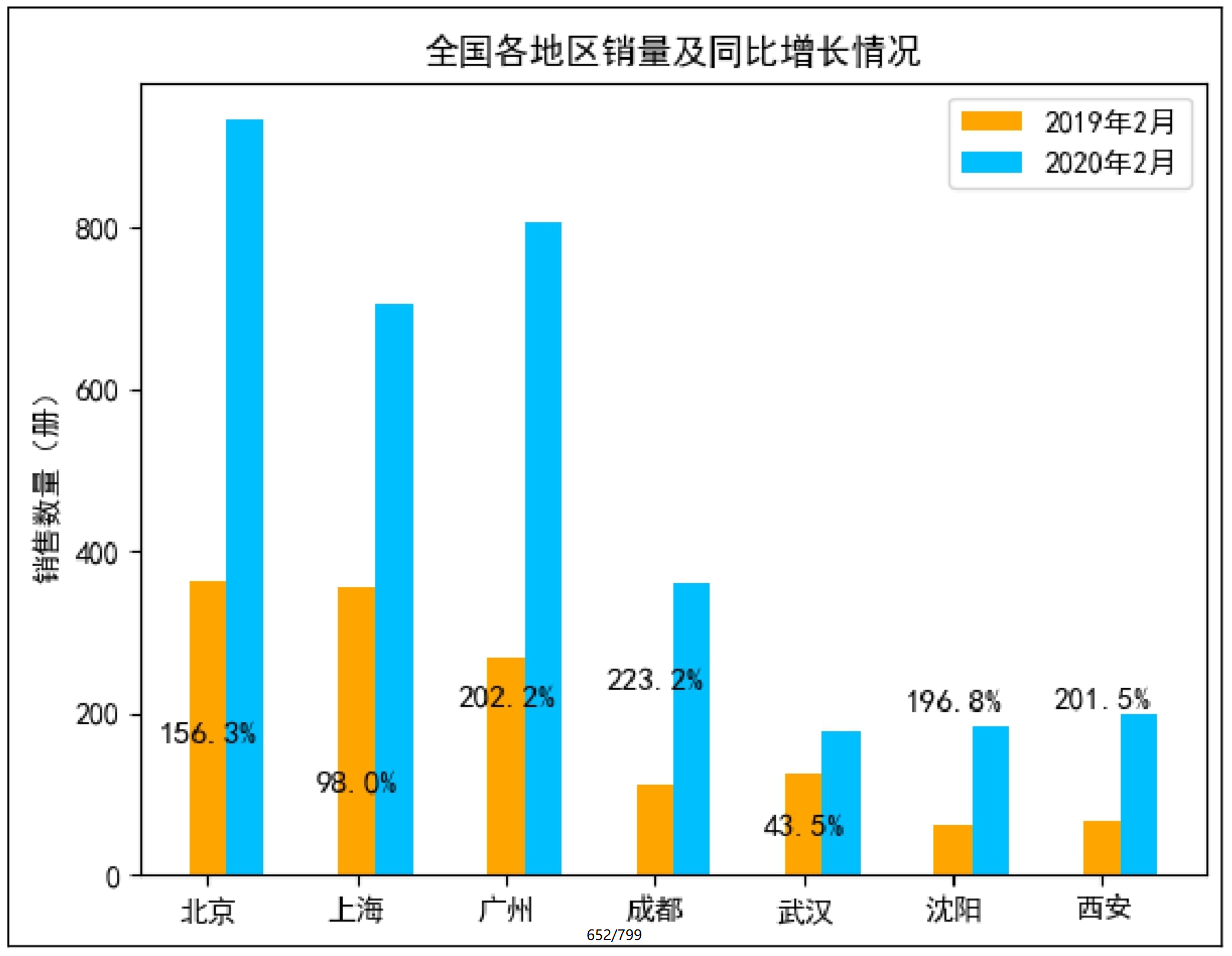
图9.2 同比分析
程序代码如下:

9.2.3 案例2:单品销量定比分析
案例位置:资源包\MR\Code\09\example\02\02
下面实现京东电商《零基础学Python(全彩版)》一书2019年销量定比分析,以2019年1月为基期,基点为1,效果如图9.3所示。
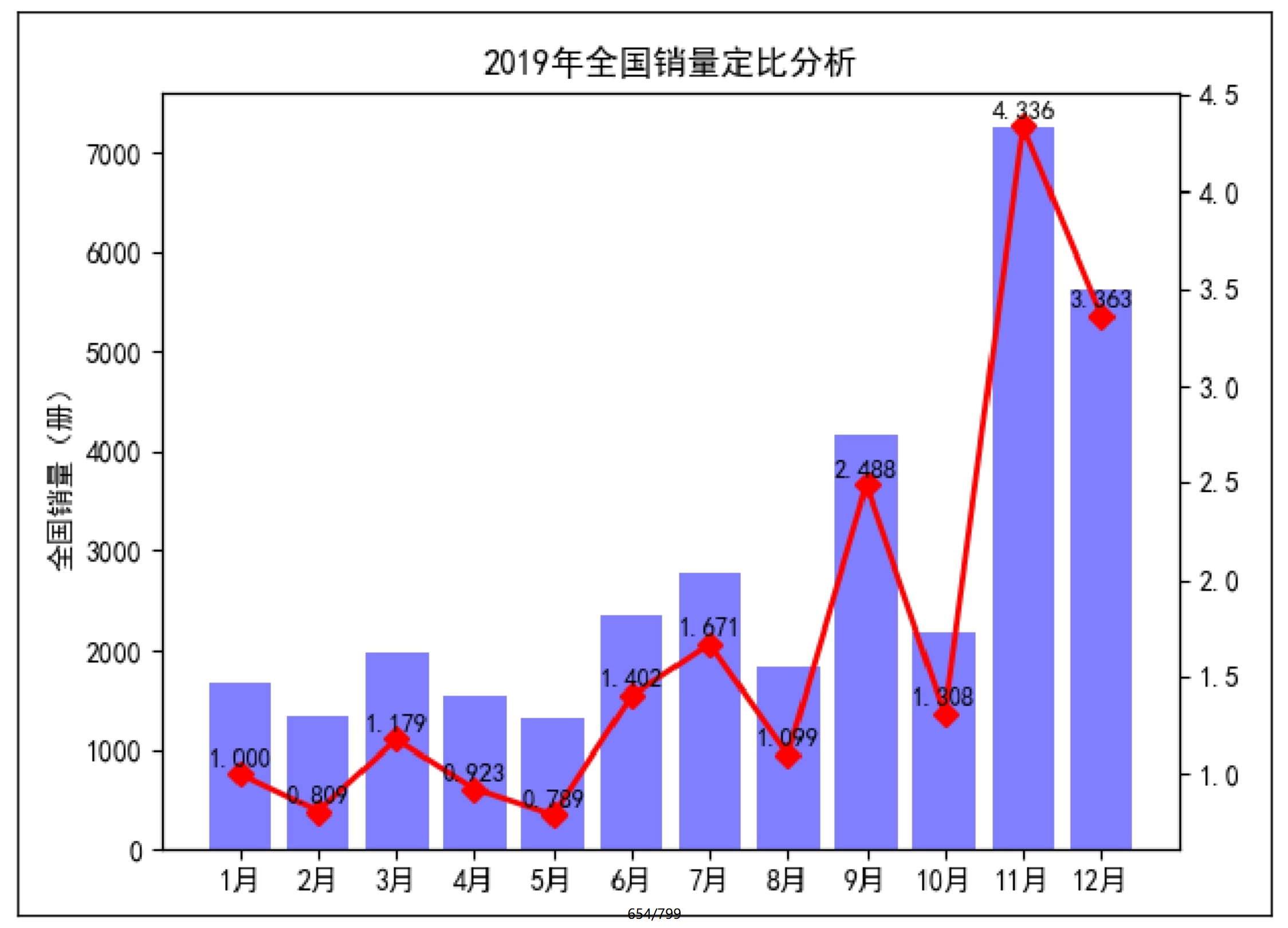
图9.3 定比分析
从图9.3中可以看到,6月开始呈现连续小幅度增长,到11月开始大幅度增长,定比指数较10月提高了3.028个点。
程序代码如下:

9.2.4 案例3:单品销量环比增长情况分析
案例位置:资源包\MR\Code\09\example\02\03
下面分析京东电商《零基础学Python(全彩版)》一书2019年销量环比增长情况,效果如图9.4所示。
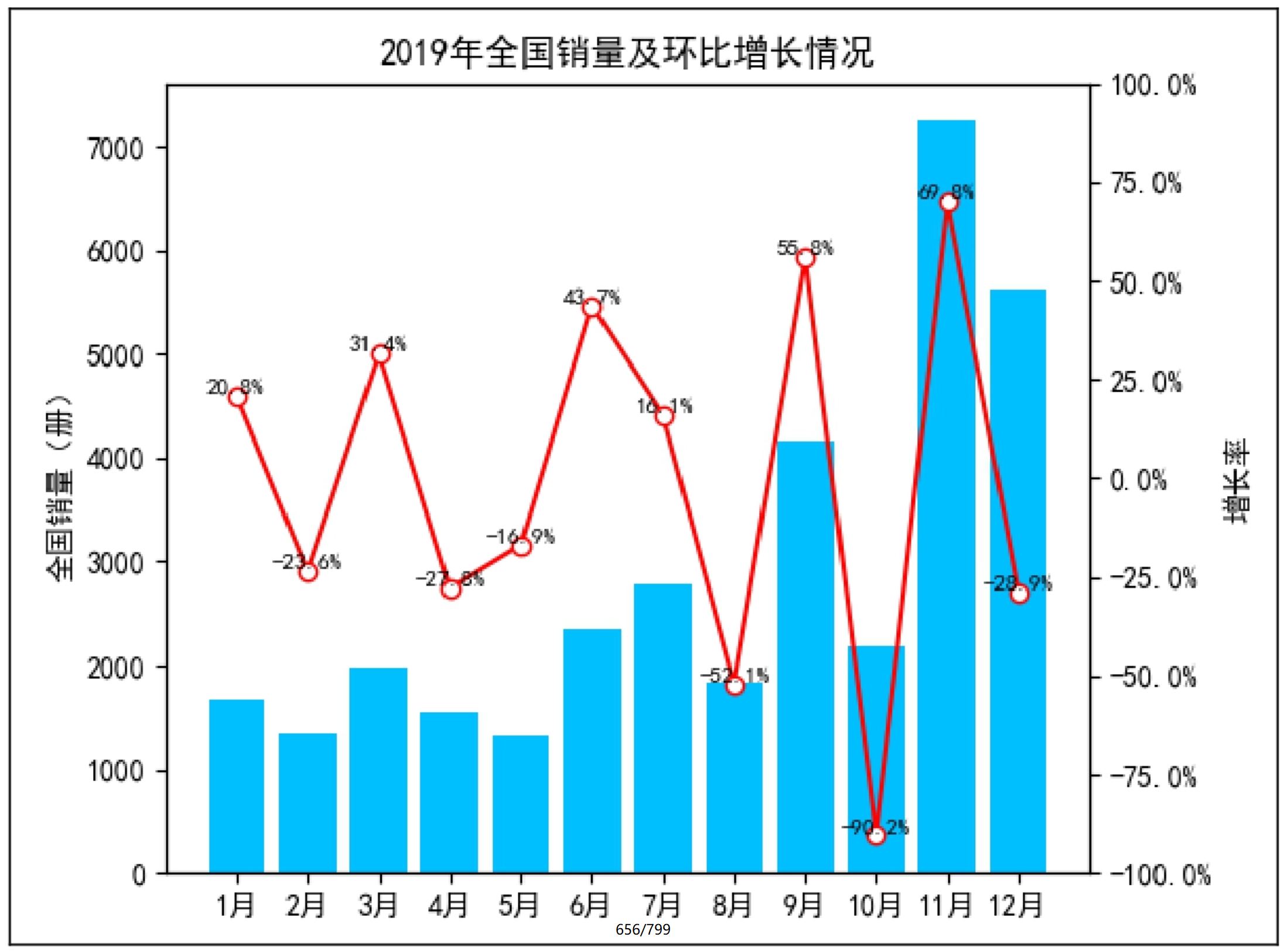
图9.4 环比分析
程序代码如下:

实用技巧
在使用Matplotlib绘制图表时,发现了一个警告Warining,如图9.5所示。

图9.5 警告信息
完整警告信息如下:
MatplotlibDeprecationWarning:
Adding an axes using the same arguments as a previous axes currently reuses the earlier instance. In a future version, a new instance will always be created and returned. Meanwhile, this warning can be suppressed, and the future behavior ensured, by passing a unique label to each axes instance.
“Adding an axes using the same arguments as a previous axes “
解决方法:
出现上述警告,原因是在创建画布fig=plt.figure()后就设置了图表标题或坐标轴标签,将图表标题或坐标轴标签相关代码放置在定义子图ax=fig.add_subplot(111)代码后就不会出现警告信息了。
9.3 贡献度分析(帕累托法则)
9.3.1 什么是贡献度分析
贡献度分析又称80/20法则、二八法则、帕累托法则、帕累托定律、最省力法则或不平衡原则。
该法则是由意大利经济学家“帕累托”提出的。80/20法则认为:原因和结果、投入和产出、努力和报酬之间本来存在着无法解释的不平衡。例如,一个公司80%的利润常常来自20%的产品,那么使用贡献度分析就可以分析获利最高的20%的产品。
下面简单介绍一下贡献率相关算法。

通过上述公式得出累计贡献率,当累计贡献率接近80%时(不一定正好是80%),然后找到该产品在图表中相应的位置并进行标注。说明
真正的比例不一定正好是80%:20%。80/20法则表明在多数情况下该关系很可能是不平衡的,并且接近于80/20。
9.3.2 案例:产品贡献度分析
案例位置:资源包\MR\Code\09\example\03
下面分析淘宝电商全彩系列图书2018年上半年销售收入占比80%的产品。首先,使用9.3.1节中的公式计算产品累计贡献率,结果如图9.6所示。从图9.6中可以看出,到图书编号B13时,累计贡献率就已达到了0.817665(接近总销售收入的80%),其中共有10种产品,接下来在图表中进行标注,如图9.7所示。
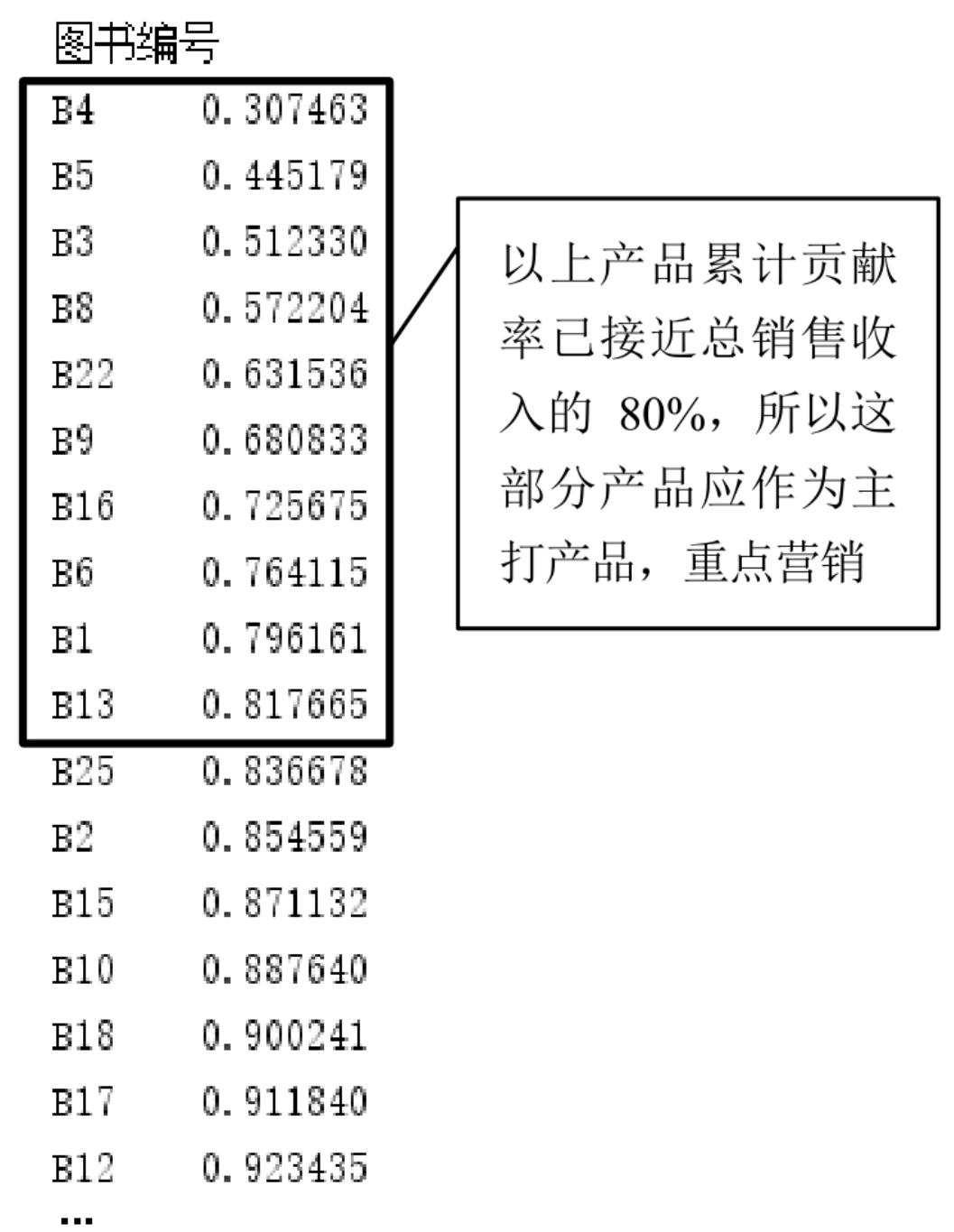
图9.6 输出累计贡献率
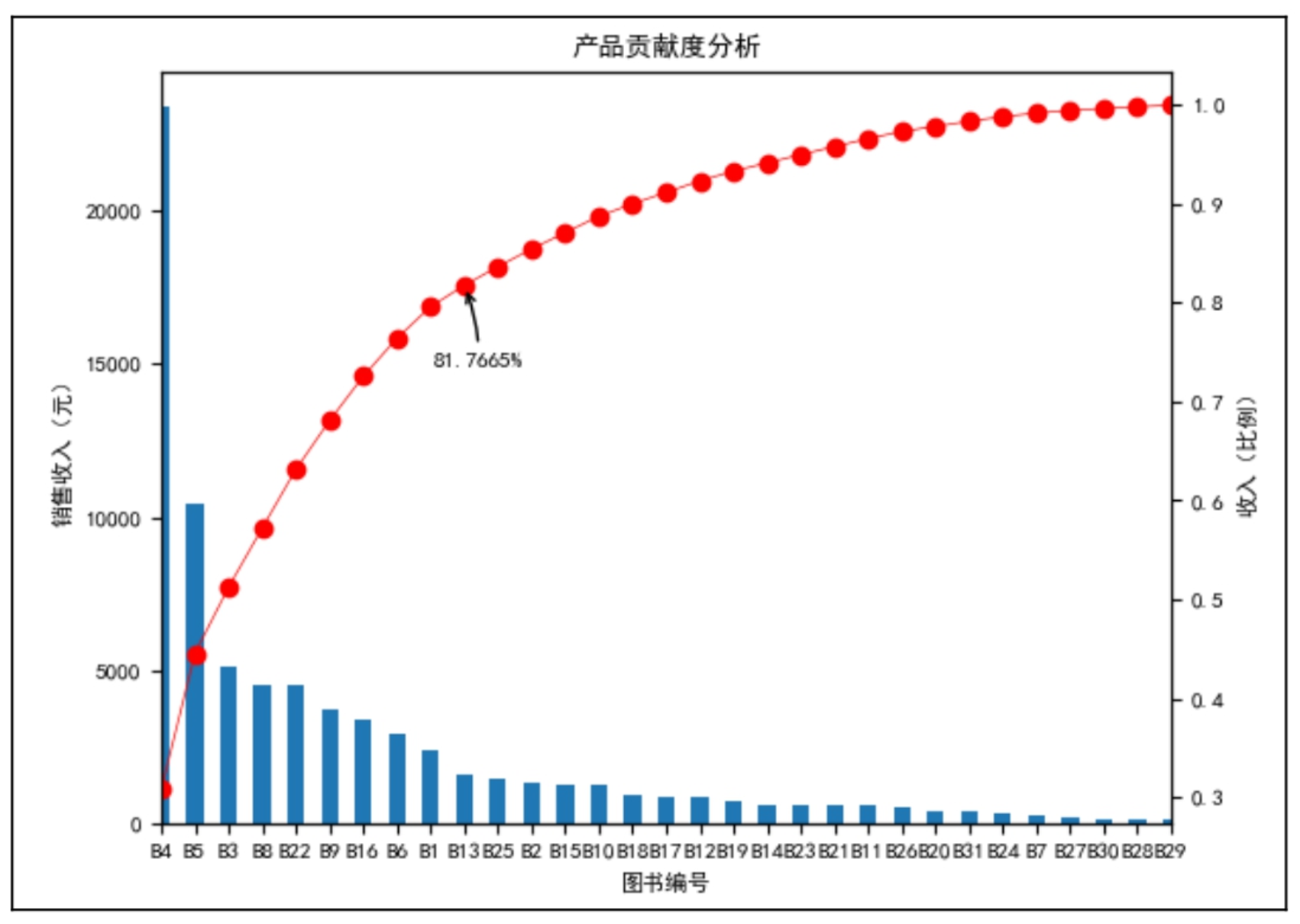
图9.7 产品贡献度分析
程序代码如下:

9.4 差异化分析
9.4.1 差异化概述
任何事物都存在差异,如同上课听讲,有人津津有味,有人昏昏欲睡。
那么,通过差异化分析,比较不同事物之间在某个指标上存在的差异,根据差异定制不同的策略。对于产品而言,差异化分析是指企业在其提供给顾客的产品上,通过各种方法满足顾客的偏好,使顾客能够把它同其他竞争企业提供的同类产品有效地区别开来,从而使企业在市场竞争中占据有利的地位。
比较常见的有性别差异、年龄差异。通过差异化分析比较不同性别之间在某个指标上存在的差异,通过分析结果对不同性别定制不同的方案。例如,分析不同性别的同学在学习成绩上的差异,了解男生和女生之间的这些差异,因材施教,定制不同的弥补弱项的方案。对于女生,可以有意识地培养她的思维能力;而对于男生,可以买些书籍,来增强他薄弱的方面。
年龄差异化分析,了解不同年龄的需求,投其所好,使企业的利润最大化。例如,网购、自媒体、汽车、旅游等行业,通过年龄差异化分析,找出不同年龄段用户群体的喜好,从而增加产品销量。
9.4.2 案例:学生成绩性别差异分析
案例位置:资源包\MR\Code\09\example\04
“女孩喜欢毛绒玩具,男孩喜欢车”这大概是天生的。
科学研究表明,男孩和女孩的差别在相当程度上是由生理基础决定的。通过高科技扫描就可以发现,男孩和女孩的大脑都会有某些部位比对方相应的部位更发达、更忙碌。
随着孩子的成长,这种天生的性别差异就会对孩子的学习有所影响,并且不断强化。而反过来,学习的本身也在改变着大脑的机能发育。因为当孩子玩耍和学习时,相对应的脑细胞就会更加活跃且随时更新,而那些不经常使用的部分将会逐渐退化萎缩。
下面我们用数据说话,通过雷达图分析男生、女生各科成绩差异,效果如图9.8所示。
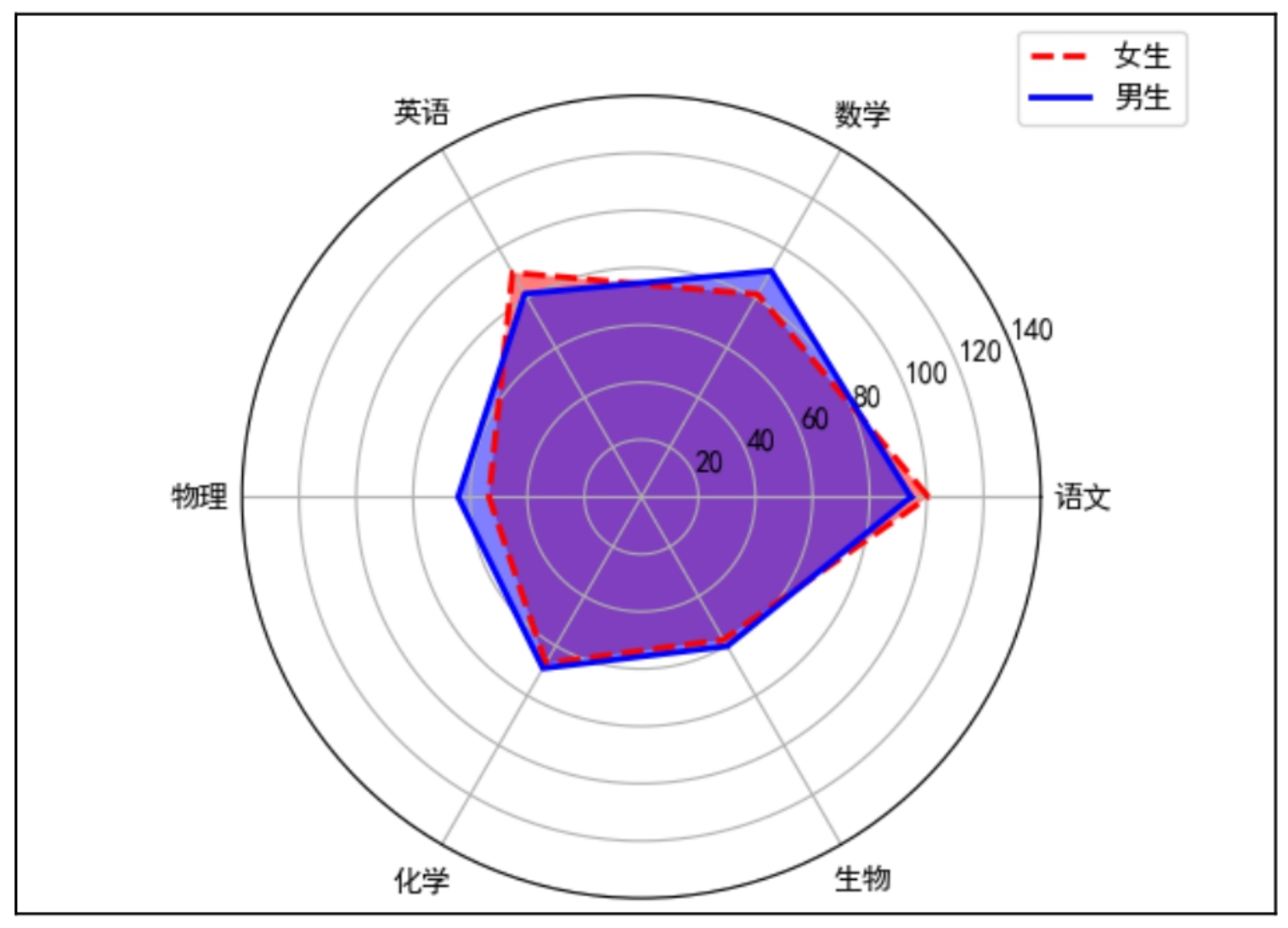
图9.8 男生、女生各科成绩差异分析
从分析结果得知:男生数学和物理高于女生,而女生在英语和语文上略占优势。针对性别差异造成学习成绩的差距,应该采取因材施教,从而提高女生的数学和物理成绩
男生的语文和英语成绩。
程序代码如下:

9.5 相关性分析
9.5.1 相关性概述
任何事物之间都存在一定的联系。例如,夏天温度的高低与空调的销量就存在相关性。当温度升高时,空调的销量也会相应提高。
相关性分析是指对多个具备相关关系的数据进行分析,从而衡量数据之间的相关程度或密切程度。相关性可以应用到所有数据的分析过程中。如果一组数据的改变引发另一组数据朝相同方向变化,那么这两组数据存在正相关性,例如,身高与体重,一般个子高的人体重会重一些,个子矮的人体重会轻一些;如果一组数据的改变引发另一组数据朝相反方向变化,那么这两组数据存在负相关性,例如,运动与体重。
9.5.2 案例:广告展现量与费用成本相关性分析
案例位置:资源包\MR\Code\09\example\05
为了促进销售,电商营销必然要投入广告,这样就会产生广告展现量和费用成本相关的数据。通常情况下,我们认为费用高,广告效果就好,它们之间必然存在联系,但仅通过主观判断没有说服力,无法证明数据之间关系的真实存在,也无法度量它们之间关系的强弱。因此,我们要通过相关性分析来找出数据之间的关系。
下面来看一下费用成本与广告展现量相关数据情况(由于数据太多,只显示部分数据),如图9.9和图9.10所示。
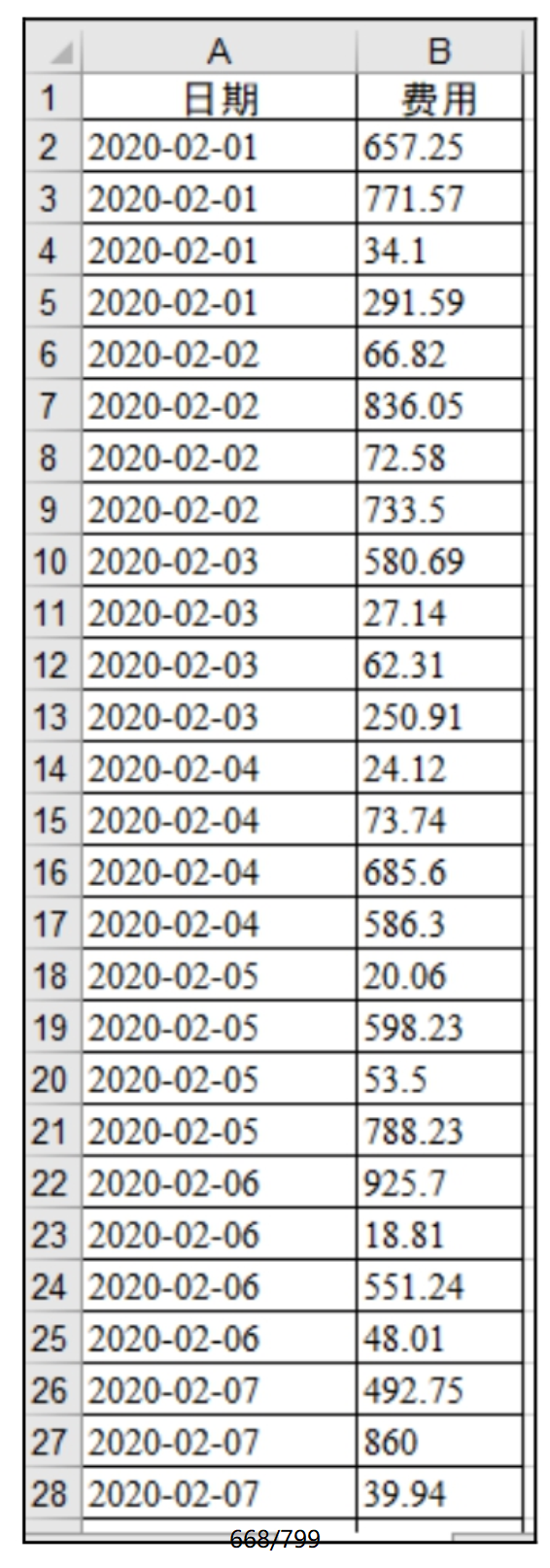
图9.9 费用成本
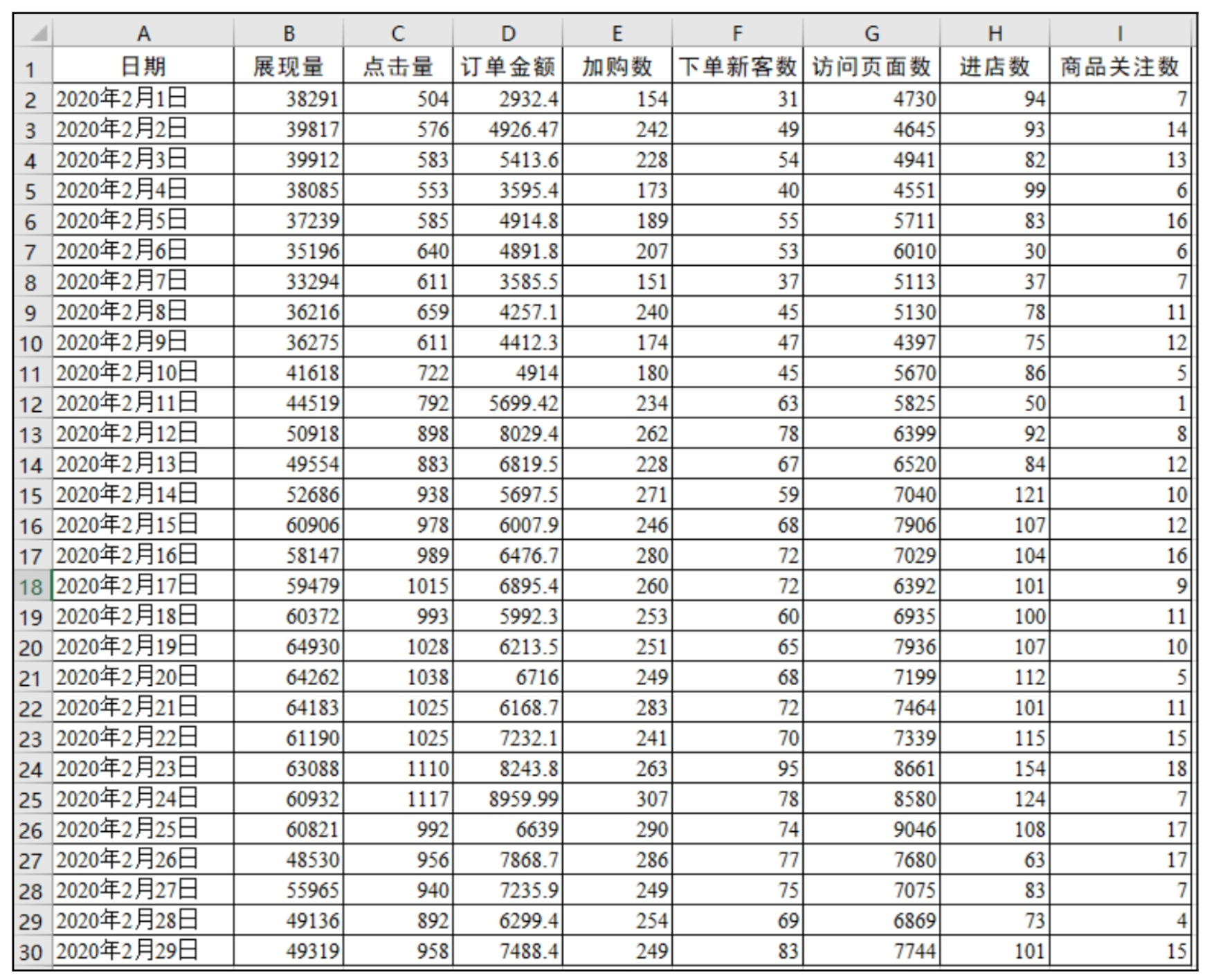
图9.10 广告展现量
相关性分析方法很多,简单的相关性分析方法是将数据进行可视化处理,单纯从数据的角度很难发现数据之间的趋势和联系,而将数据绘制成图表后就可以直观地看出数据之间的趋势和联系。
下面通过散点图看一看广告展现量与费用成本的相关性,效果如图9.11所示。
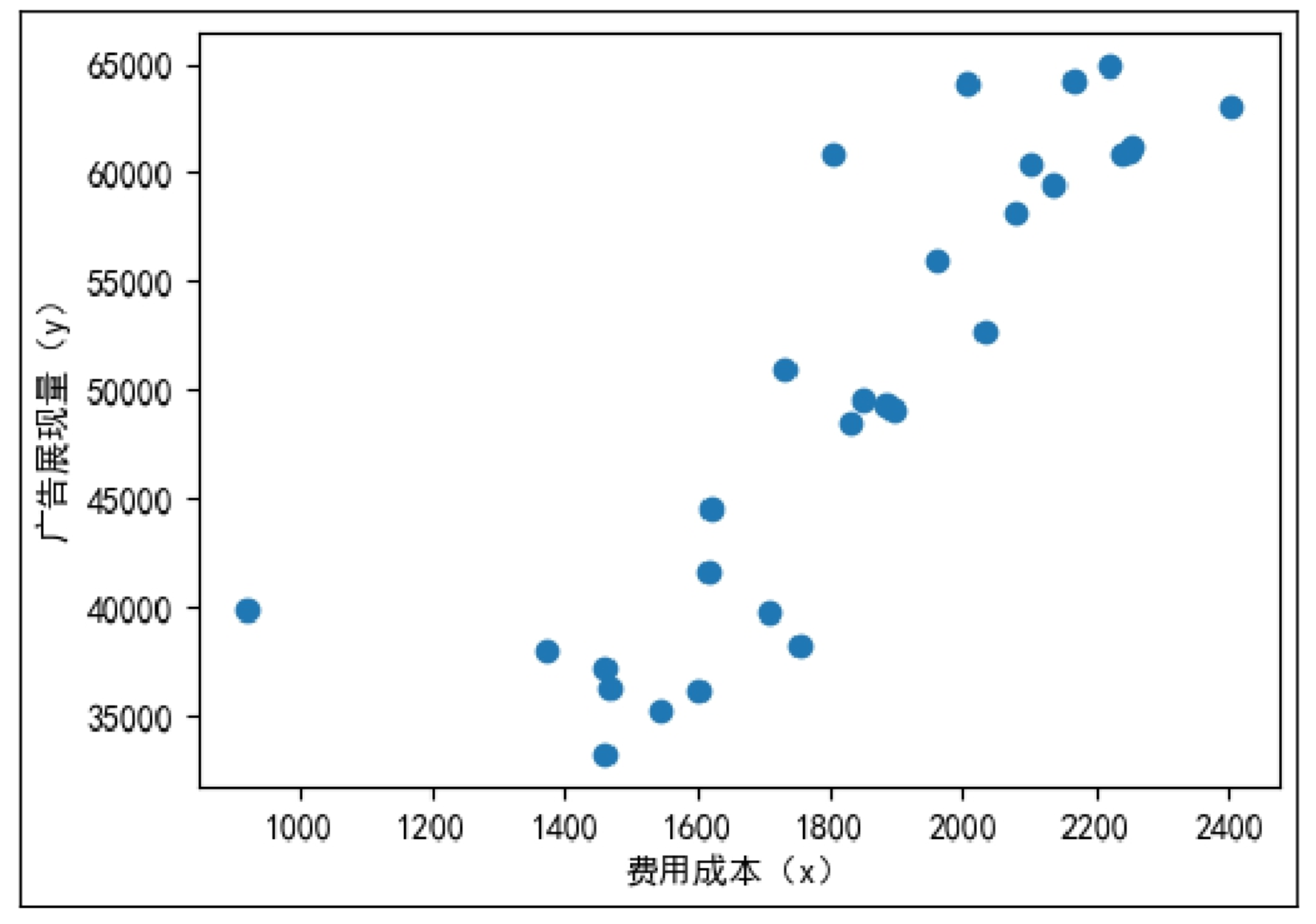
图9.11 散点图
首先对数据进行简单处理,由于“费用.xlsx”表中同一天会产生多个类型的费用,所以需要按天统计费用,然后将“展现量.xlsx”和“费用.xlsx”两张表的数据合并,最后绘制散点图,程序代码如下:

虽然图表清晰地展示了广告展现量与费用成本的相关性,但无法判断数据之间有什么关系,相关关系也没有准确地度量,并且数据超过两组时也无法完成各组数据的相关性分析。
下面再介绍一种方法——相关系数方法。相关系数是反映数据之间关系密切程度的统计指标,相关系数的取值区间为1~-1。1表示数据之间完全正相关(线性相关);-1表示数据之间完全负相关;0表示数据之间不相关。数据越接近0表示相关关系越弱,越接近1表示相关关系越强。
计算相关系数需要一定的计算公式,而在Python中无须使用烦琐的公式,通过DataFrame对象提供的corr()函数就可以轻松实现,关键代码如下:
data.corr()
运行程序,输出结果如图9.12所示。
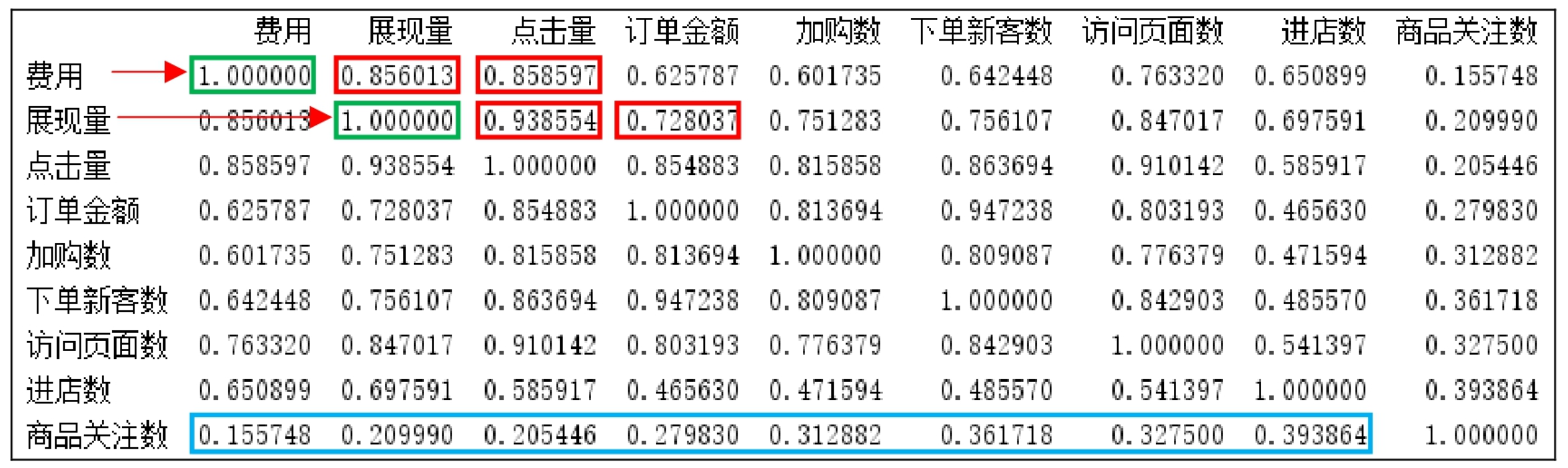
图9.12 各组数据的相关系数
从分析结果得知:“费用”与“费用”自身的相关性是1,与“展现量”“点击量”的相关系数分别是0.856013、0.858597;“展现量”与“展现量”自身的相关性是1,与“点击量”“订单金额”的相关系数分别是0.938554、0.728037。那么,除了“商品关注数”相关系数比较低,其他都很高,可以看出“费用”与“展现量”“点击量”等有一定的正相关性,而且相关性很强。
相关系数的优点是可以通过数字对变量的关系进行度量,并且带有方向性,1表示正相关,-1表示负相关,越靠近0相关性越弱。缺点是无法利用这种关系对数据进行预测。
9.6 时间序列分析
9.6.1 时间序列概述
顾名思义,时间序列就是按照时间顺序排列的一组数据序列。时间序列分析就是找出数据变化发展的规律,从而预测未来的走势。
时间序列分析有以下几种表现形式。
长期趋势变化:受某种因素的影响,数据依据时间变化,按某种规则稳步增长或下降。使用的分析方法有移动平均法、指数平滑法等。
季节性周期变化:受季节更替等因素影响,数据依据固定周期规则性的变化。季节性周期变化,不局限于自然季节,还包括月、周等短期周期。例如,空调、羽绒服、冷饮的销售,双十一、双十二流量在一周之内的波动等。采用的方法为季节指数。
循环变化:指一种较长时间的上、下起伏周期性波动,一般循环时间为2~15年。
随机性变化:由许多不确定因素引起的数据变化,在时间序列中无法预计。
9.6.2 案例:年增长趋势和季节性波动分析
案例位置:资源包\MR\Code\09\example\06
下面分析淘宝店铺近3年增长趋势和季节性波动,如图9.13所示。从分析结果得出,近3年淘宝店铺收入呈现持续稳定增长趋势,但2019年有所下降,季节性波动比较明显,每年的第4季度是销售“旺季”。
程序代码如下:

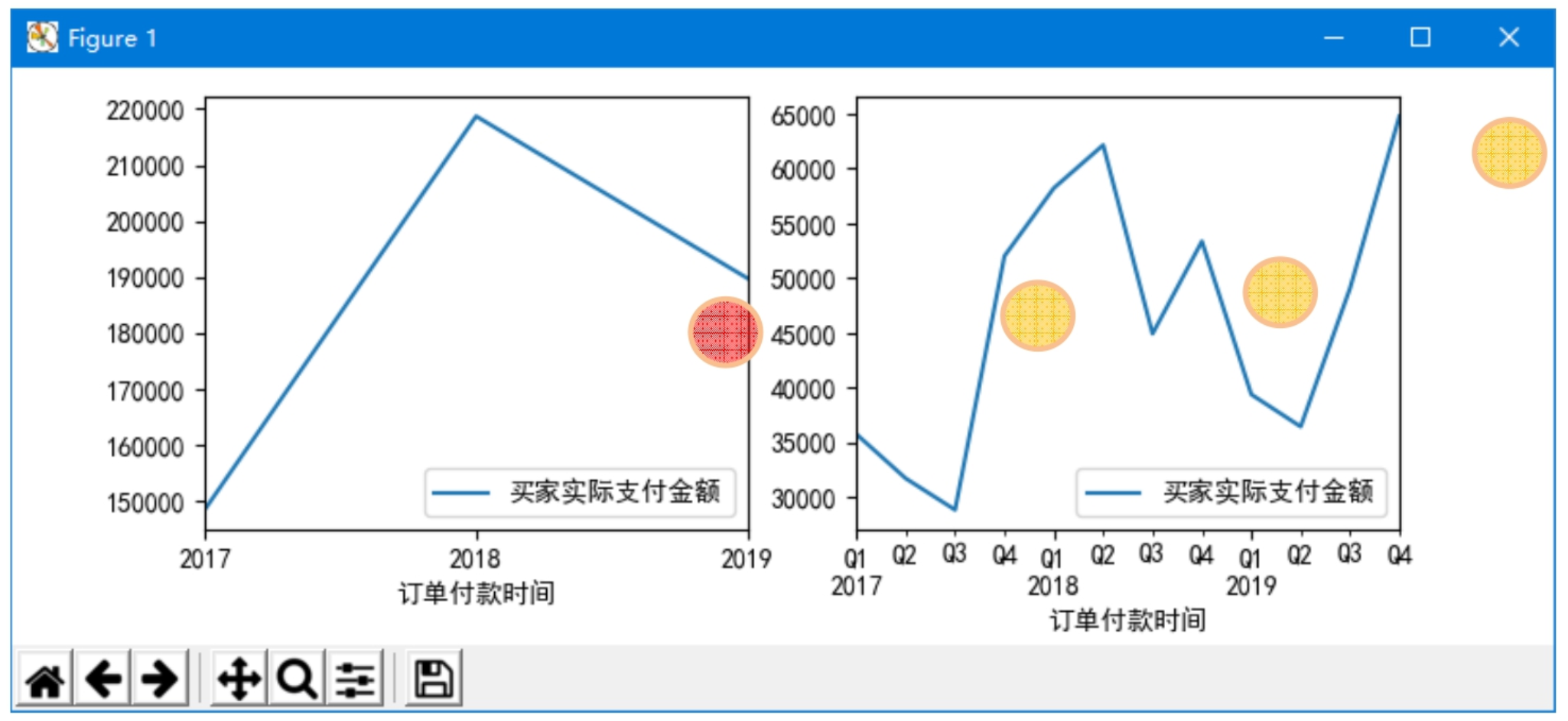
图9.13 年增长趋势和季节性波动
9.7 小结
本章通过常用的数据分析方法并结合图表,以案例的形式呈现,每一种分析方法都对应一个恰当的分析案例,一张贴切的图表,力求使读者能够真正理解数据分析,并将其应用到实际数据分析工作中。每一个案例都经过作者反复揣摩,希望能够对读者有所帮助。
- 本文作者: 不想
- 本文链接: https://evacat.top/2020/05/15/第9章数据统计分析案例/
- 版权声明: 本博客所有文章除特别声明外,均采用 MIT 许可协议。转载请注明出处!



